
When driving a conveyor drive motor with a variable frequency drive (VFD) it is essential that the operator/designer be aware of all required powers and all available powers at all relevant rates.
ABOUT RULMECA CORPORATION
We supply Motorized Pulley belt conveyor drives, serving equipment manufacturers directly and end users through a network of independent distributors & local service providers throughout the United States and Latin America.
The 10 HP motor shown above (left), designed to run on 460v/3ph/60Hz, draws 12.1 amps when the motor is running at full load. Current at full load is “full load amps” (FLA). The motor on the right shows an even, generalized burn of the stator wires due to overstress.
Each AC Squirrel Cage Induction Motor is optimized to run at a certain power supply and carry a specified FLA. It has no inherent ability to protect itself from current overload. Current overload will occur when required power exceeds available power

A constant force of F, exerting itself on a point that moves a displacement of S, defines the work done.
Work = Force x displacement
W = Fs
If F = 1,000 lbs and s = 330 ft, then
Work = 1,000 lbs x 330 ft
Work = 330,000 ft-lbs

Power is the rate of doing work. Power equals force times displacement per unit of time.
Power = (Force x displacement)/time
Power = Fs/t
If a force of 1,000 lbs, exerts itself on a point in a straight line for 330 ft and it takes 1 minute, then
Required power = (1,000 lbs x 330 ft)/1 minute
Required power = 330,000 ft-lbs/min
In conveyor technology, this equation is more useful.
Power = Force x velocity
Power = F(s/t)
Required power = 1,000 lbs x 330 FPM
Required power = 330,000 ft-lbs/min
Since 1 HP = (33,000 ft-lbs/min)/HP
Required power = 330,000/33,000 = 10 HP
In bulk handling applications
Required power = belt pull x belt speed
Belt Pull = 1,000 lbs
Belt Speed = 330 fpm
Required power = 1,000 x 330 = 330,000 ft-lbs/min
Since 1 HP = 33,000 ft-lbs/min
Required power = 330,000/33,000 = 10 HP
To simplify this explanation, we have ignored mechanical gear losses.
When selecting a motor, a power supply must be specified (e.g. 460v/3ph/60Hz).

To explain synchronous speed of an AC motor, its supply frequency must be defined. AC current reverses polarity once per cycle.
1 cycle per second = 1 Hertz
If supply frequency is 60 Hz, polarity reverses 60 times per second.
A 3 phase AC squirrel cage induction motor consists of a stator and a rotor. A “2-pole motor” has two poles in the stator and two poles in the rotor. As current flows through the stator wires at 60 Hz, the stator’s magnetic flux forces the rotor rotate 60 times/second. Synchronous 2-pole rotor RPM (revolutions per minute) is:
2-pole Rotor RPM = 60 revolutions/second x 60 seconds/minute
2-pole Rotor RPM = 3,600 RPM
All motors described in this blog are “asynchronous motors”, designed to “slip”, but we are ignoring that to make the concepts easier to grasp.
A Motorized Pulley conveyor drive encloses all moving electrical and mechanical components within a pulley shell.
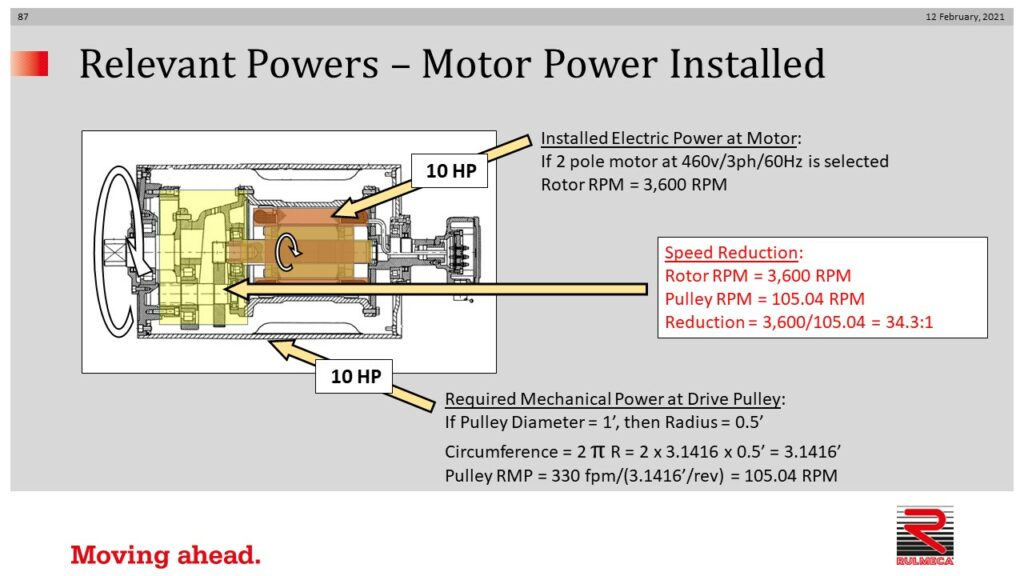
Pulley RPM = belt speed/pulley circumference
Pulley RPM = (330 fpm)/(3.1416 ft/revolution) = 105.04
If a 2-pole motor drives the system on a 60 Hz power supply, rotor RPM = 3,600 RPM.
Speed reduction = rotor RPM/pulley RPM
Speed reduction = 3,600/105.04 = 34.3:1

Conveyors require power to move in a straight line. Motors apply power by spinning. Note the difference between belt pull and torque.
Required power = force x velocity
Installed power = torque x angular velocity
If required belt pull = 1,000 lbs and belt speed = 330 FPM,
Required power = 1,000 lbs x 330 FPM
Required power = 330,000 ft-lbs/min
Since 1 HP = 33,000 ft-lbs/min
Required power = 330,000/33,000 = 10 HP
If a 10 HP electric motor and speed reducer drive a 1 ft diameter pulley at 105.04 RPM
Installed power = 10 HP
Installed power = torque x angular velocity
Torque = Installed power/angular velocity
Angular velocity = RPM x 2π radians/rev
Torque = (330,000 ft-lbs/min)/(105.04 x 6.2832)
Torque = 500 ft-lbs
Installed motor torque = power/angular velocity
If motor is 10 HP
Motor torque = (330,000 ft-lbs/min)/(3,600 RPM x 2π radians/rev)
Motor torque = 14.59 ft-lbs
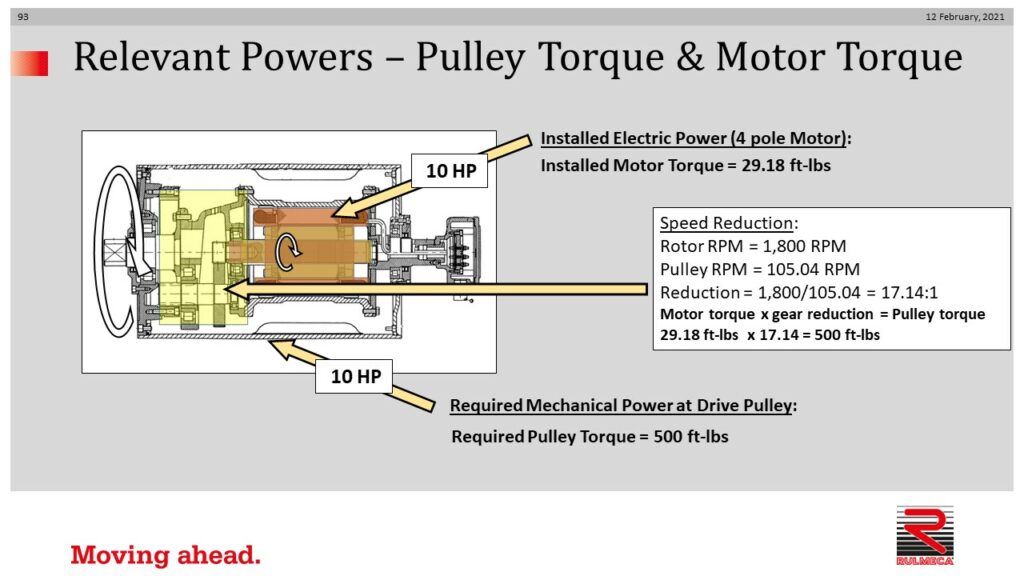
Pulley torque = torque at pulley face. Gear reduction = rotor RPM/pulley RPM. In our example, reduction is 34.3:1.
If torque at pulley face is 500 ft-lbs,
Motor rotor torque = 500 ft-lbs/34.3
Motor rotor torque = 14.59 ft-lbs
